归并排序

归并排序采用经典的分治策略，利用归并的思想实现的排序方法。把一个待排序的数组无限拆分，直到子数组只有一个元素，然后开始按顺序再进行合并。想象一下若一副扑克牌乱序混在一起，如何从小到大排序？

1. 把牌堆分层两份，分给两个小伙伴进行从小到大排序。
2. 两位小伙伴排序完成，给到有序牌堆A和有序牌堆B。
3. 每次抽取两个牌堆最顶端一张进行比较，较小的合入到整体有序的牌堆C中。

那么两个小伙伴是如何把分到的扑克牌给排序完成的呢？

1. 把牌堆分层两份，分给两个小伙伴进行从小到大排序。

2. 两位小伙伴排序完成，给到有序牌堆A和有序牌堆B。

3. 每次抽取两个牌堆最顶端一张进行比较，较小的合入到整体有序的牌堆C中。

那么两个小伙伴是如何把分到的扑克牌给排序完成的呢？

重复步骤1-3 ···

当某次分牌时，某两位小伙伴各自仅分到了一张牌，那就不能再继续分了，他俩把分到的牌按照大小顺序交上去，这样就有了有序的牌堆（2张牌），然后2张合4张，4张合8张···，到最后整副扑克牌都是有序的。

这就是归并的思想

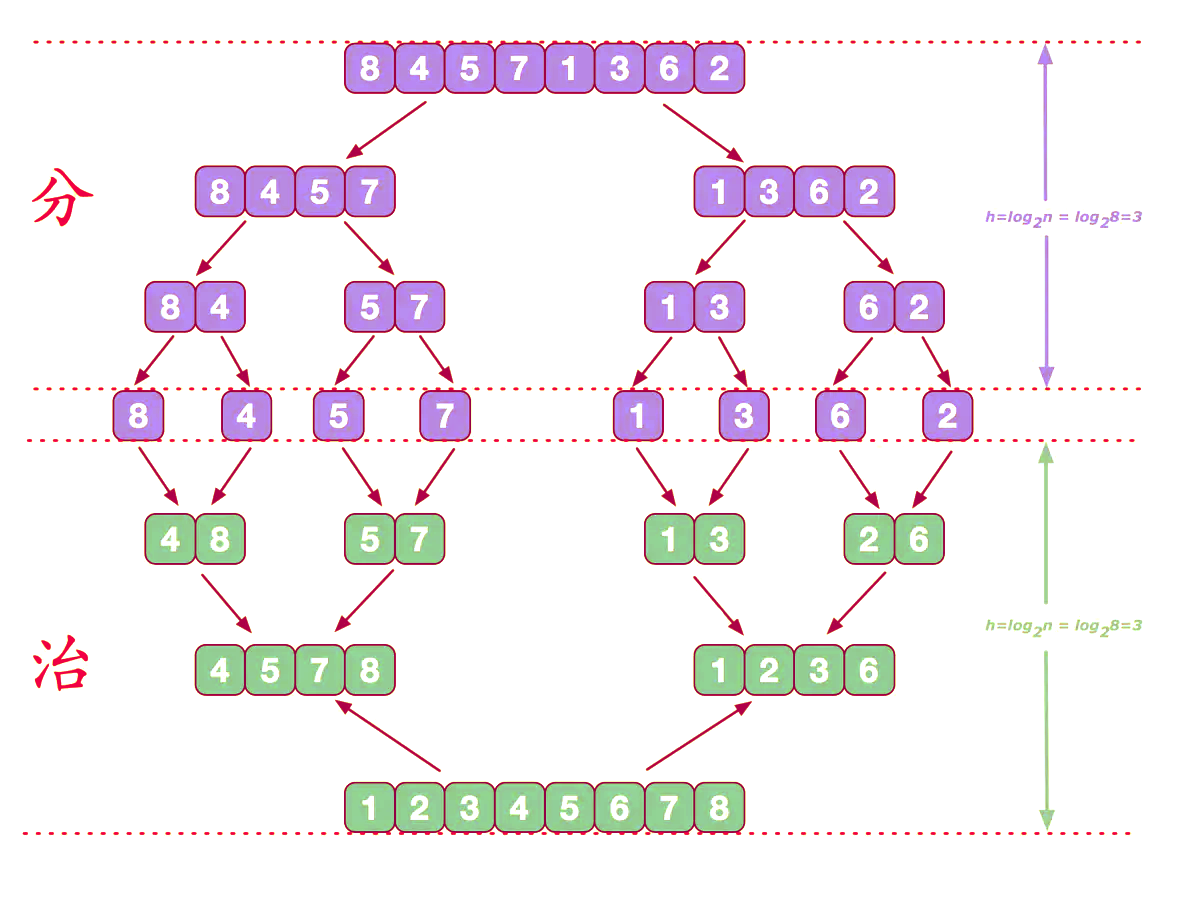
动图理解：

代码实现：

/**
 * @param arr  带排序的数组
 * @param low  数组中较低的一侧的下标
 * @param high 数组中较高的一侧的下标
 */
public static void mergeSort(int[] arr, int low, int high) {
    int middle = (high + low) / 2;
    if (low < high) {
        // 处理左边
        mergeSort(arr, low, middle);
        // 处理右边
        mergeSort(arr, middle + 1, high);
        // 合并左右两边
        merge(arr, low, middle, high);
    }
}

/**
 * @param arr    待归并的数组
 * @param low    左侧数组起始位置
 * @param middle 左侧数组的结束位置
 * @param high   右侧数组结束位置
 */
private static void merge(int[] arr, int low, int middle, int high) {
    // 用于存储归并后的临时数组
    int[] temp = new int[high - low + 1];
    // 记录第一个数组中需要遍历的下标
    int i = low;
    // 记录第二个数组中需要遍历的下标
    int j = middle + 1;
    // 用于记录在临时数组中存放的下标
    int index = 0;
    while (i <= middle && j <= high) {
        if (arr[i] <= arr[j]) {
            temp[index++] = arr[i++];
        } else {
            temp[index++] = arr[j++];
        }
    }
    // 一个数组中的数已经全部放入temp,剩下较长的一个子数组的数全部放进temp中
    while (j <= high) {
        temp[index++] = arr[j++];
    }
    while (i <= middle) {
        temp[index++] = arr[i++];
    }
    // 把临时数组中的数据重新存入原来数组
    for (int k = 0; k < temp.length; k++) {
        arr[k + low] = temp[k];
    }
}