2018年Coding被腾讯收购后变成了腾讯开发者平台,一直不温不火。今年一月份有又要改名为新Coding,真是命途多舛,还好提供的服务一直可以满足我的需求。虽然偶尔服务器宕机,但是速度快呀,Coding pages还是真香。由于今年网站再次改版,之前的pages要停止服务了,貌似也没有通知一声,昨天修复了一下,看了下留言,我的小站还是有人浏览的。所以决定还是要好好经营下去。
最近看了一些书,有了一些新的感悟。学习是要有输出的,只有自己能把一个东西讲清楚才算真正学会了,那么就把最近研究和学习的一些东西给写下来吧。
大学学过的一些很基础的排序算法
冒泡排序
掌握一种算法不是把它的实现代码给背下来,而是理解他的思想。这样就可以做到以不变应万变。
冒泡排序的思想是:在一个n个数的乱序数组中,遍历整个数组(n-1)轮,每次遍历位数减少1,每次选择出一个最大的数放在数组的末尾,这样在经过(n-1)轮遍历之后,数组中所有的元素都是有序的。
原理:
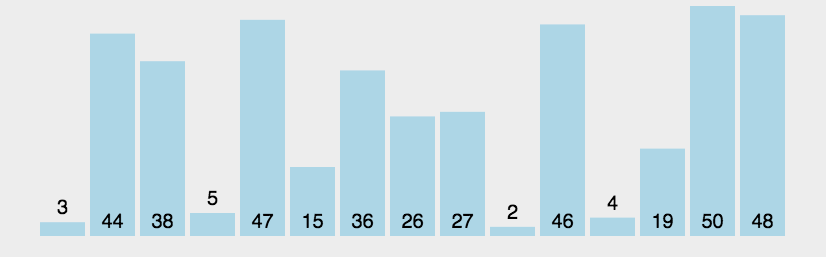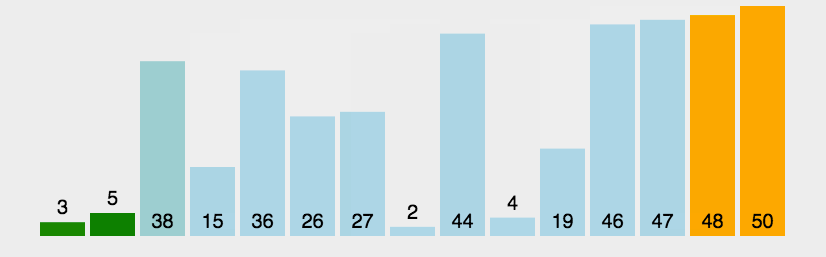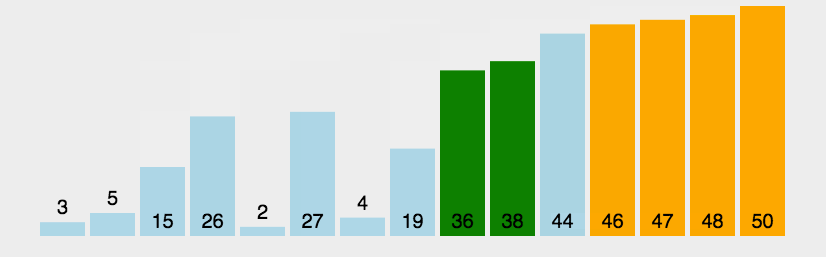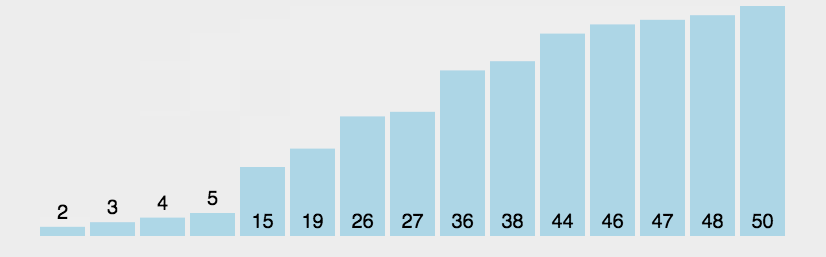
实现代码:
1
2
3
4
5
6
7
8
9
10
11
12
| public static void bubble(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j + 1] < arr[j]) {
arr[j + 1] = arr[j + 1] ^ arr[j];
arr[j] = arr[j + 1] ^ arr[j];
arr[j + 1] = arr[j + 1] ^ arr[j];
}
}
System.out.println("第" + (i) + "趟排序:" + Arrays.toString(arr));
}
}
|
上面我使用了一个不引入第三个变量,实现交换两个变量的值的技巧,一个数对另一个数进行两次异或运算得到的结果是这个数本身,交换a和b的值的方法:
1
2
3
| a = a ^ b;
b = a ^ b;
a = a ^ b;
|
那么不管是最好的情况还是最坏的情况,实际判断的次数是不会减少的,是否可以优化呢?答案是肯定的,如果在最好的情况下,可以发现,在第一趟排序中所有的数都没有发生交换。
所以可以进行如下优化,当在一轮遍历中,如果没有两个数进行交换,就可以认为整体数组是有序的,优化之后的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public static void bubble(int[] arr) {
boolean flag = false;
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j + 1] < arr[j]) {
flag = true;
arr[j + 1] = arr[j + 1] ^ arr[j];
arr[j] = arr[j + 1] ^ arr[j];
arr[j + 1] = arr[j + 1] ^ arr[j];
}
}
System.out.println("第" + (i) + "趟排序:" + Arrays.toString(arr));
if (!flag) {
break;
} else {
flag = false;
}
}
}
|
选择排序
选择排序相对冒泡排序而言,交换的次数减少了,所以效率也提高了一些。选择排序的思想是:
经过(n-1)轮遍历,依次找到每个位置上该放的值。第1次遍历找到最小的值a,把它当到第一位;第2次遍历找到除最小值a以外的最小值b,把它放到第二位··· 直到(n-1)次遍历,找到最小值把它放到(n-1)位,即第倒数二位。此时数组为全局有序。
原理:

代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
int min = arr[i];
for (int j = i + 1; j < arr.length; j++) {
if (min > arr[j]) {
min = arr[j];
minIndex = j;
}
}
if (minIndex != i) {
arr[minIndex] = arr[i];
arr[i] = min;
}
}
}
|
插入排序
选择排序的思想是找位置,与选择排序不同,插入排序的思想是找一个有序的区间,保证这个区间内是有序的。通过一次次的遍历,逐渐扩大这个有序区间,直到区间大小等于数组大小,即数组全局有序。所谓逐渐扩大,即把待插入的数,插入到有序区间内属于这个数的恰当位置。
原理:
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public static void insertSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int insertVal = arr[i];
int insertIndex = i - 1;
while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
arr[insertIndex + 1] = arr[insertIndex];
insertIndex--;
}
arr[insertIndex + 1] = insertVal;
System.out.println("第" + i + "轮插入");
System.out.println(Arrays.toString(arr));
}
}
|